4. Первые попытки прогнозирования оттока
Посмотрим, как отток связан с признаком "Подключение международного роуминга" (International plan). Сделаем это с помощью сводной таблички crosstab, а также путем иллюстрации с Seaborn (как именно строить такие картинки и анализировать с их помощью графики – материал следующей статьи).
pd.crosstab(df['Churn'], df['International plan'], margins=True)
| International plan | False | True | All |
|---|---|---|---|
| Churn | |||
| --- | --- | --- | --- |
| 0 | 2664 | 186 | 2850 |
| 1 | 346 | 137 | 483 |
| All | 3010 | 323 | 3333 |
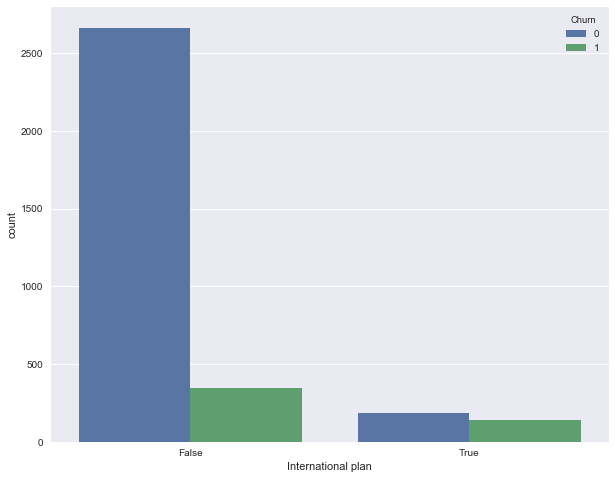
Видим, что когда роуминг подключен, доля оттока намного выше – интересное наблюдение! Возможно, большие и плохо контролируемые траты в роуминге очень конфликтогенны и приводят к недовольству клиентов телеком-оператора и, соответственно, к их оттоку.
Далее посмотрим на еще один важный признак – "Число обращений в сервисный центр" (Customer service calls). Также построим сводную таблицу и картинку.
pd.crosstab(df['Churn'], df['Customer service calls'], margins=True)
| Customer service calls | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | All |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Churn | |||||||||||
| --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| 0 | 605 | 1059 | 672 | 385 | 90 | 26 | 8 | 4 | 1 | 0 | 2850 |
| 1 | 92 | 122 | 87 | 44 | 76 | 40 | 14 | 5 | 1 | 2 | 483 |
| All | 697 | 1181 | 759 | 429 | 166 | 66 | 22 | 9 | 2 | 2 | 3333 |
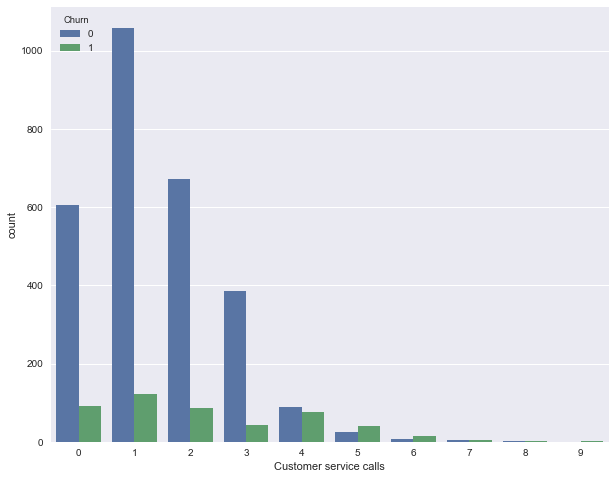
Может быть, по сводной табличке это не так хорошо видно (или скучно ползать взглядом по строчкам с цифрами), а вот картинка красноречиво свидетельствует о том, что доля оттока сильно возрастает начиная с 4 звонков в сервисный центр.
Добавим теперь в наш DataFrame бинарный признак — результат сравнения Customer service calls > 3. И еще раз посмотрим, как он связан с оттоком.
df['Many_service_calls'] = (df['Customer service calls'] > 3).astype('int')
pd.crosstab(df['Many_service_calls'], df['Churn'], margins=True)
| Churn | 0 | 1 | All |
|---|---|---|---|
| Many_service_calls | |||
| --- | --- | --- | --- |
| 0 | 2721 | 345 | 3066 |
| 1 | 129 | 138 | 267 |
| All | 2850 | 483 | 3333 |
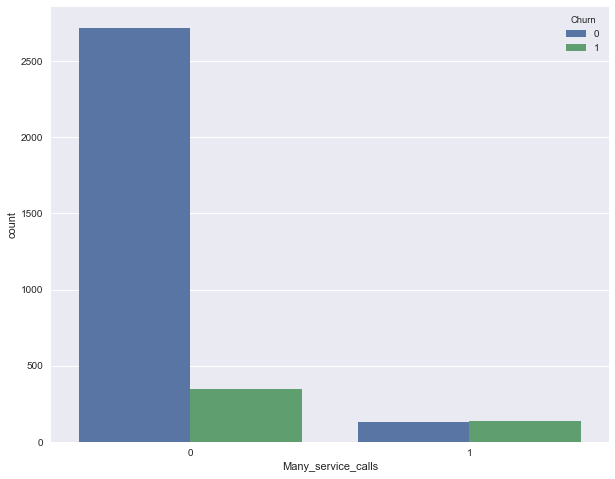
Объединим рассмотренные выше условия и построим сводную табличку для этого объединения и оттока.
pd.crosstab(df['Many_service_calls'] & df['International plan'] , df['Churn'])
| Churn | 0 | 1 |
|---|---|---|
| row_0 | ||
| --- | --- | --- |
| False | 2841 | 464 |
| True | 9 | 19 |
Значит, прогнозируя лояльность клиента в случае, когда число звонков в сервисный центр меньше 4 и не подключен роуминг (и прогнозируя отток – в противном случае), можно ожидать процент "угадывания лояльности клиента" около 85.8% (ошибаемся всего 464 + 9 раз). Эти 85.8%, которые мы получили с помощью очень простых рассуждений – это неплохая отправная точка (baseline) для дальнейших моделей машинного обучения, которые мы будем строить.
В целом до появления машинного обучения процесс анализа данных выглядел примерно так. Прорезюмируем:
- Доля лояльных клиентов в выборке – 85.5%. Самая наивная модель, ответ которой "клиент всегда лоялен" на подобных данных будет угадывать примерно в 85.5% случаев. То есть доли правильных ответов (accuracy) последующих моделей должны быть как минимум не меньше, а лучше, значительно выше этой цифры;
- С помощью простого прогноза, который условно можно выразить такой формулой: "International plan = False & Customer Service calls < 4 => Churn = 0, else Churn = 1", можно ожидать долю угадываний 85.8%, что еще чуть выше 85.5%. Впоследствии мы поговорим о деревьях решений и разберемся, как находить подобные правила автоматически на основе только входных данных;
- Эти два бейзлайна мы получили без всякого машинного обучения, и они служат отправной точной для наших последующих моделей. Если окажется, что мы громадными усилиями увеличиваем долю правильных ответов всего, скажем, на 0.5%, то возможно, мы что-то делаем не так, и достаточно ограничиться простой моделью из двух условий;
- Перед обучением сложных моделей рекомендуется немного покрутить данные и проверить простые предположения. Более того, в бизнес-приложениях машинного обучения чаще всего начинают именно с простых решений, а потом экспериментируют с их усложнениями.